Difracción de la luz y las vías del metro

La luz viaja en línea recta… excepto cuando no lo hace.

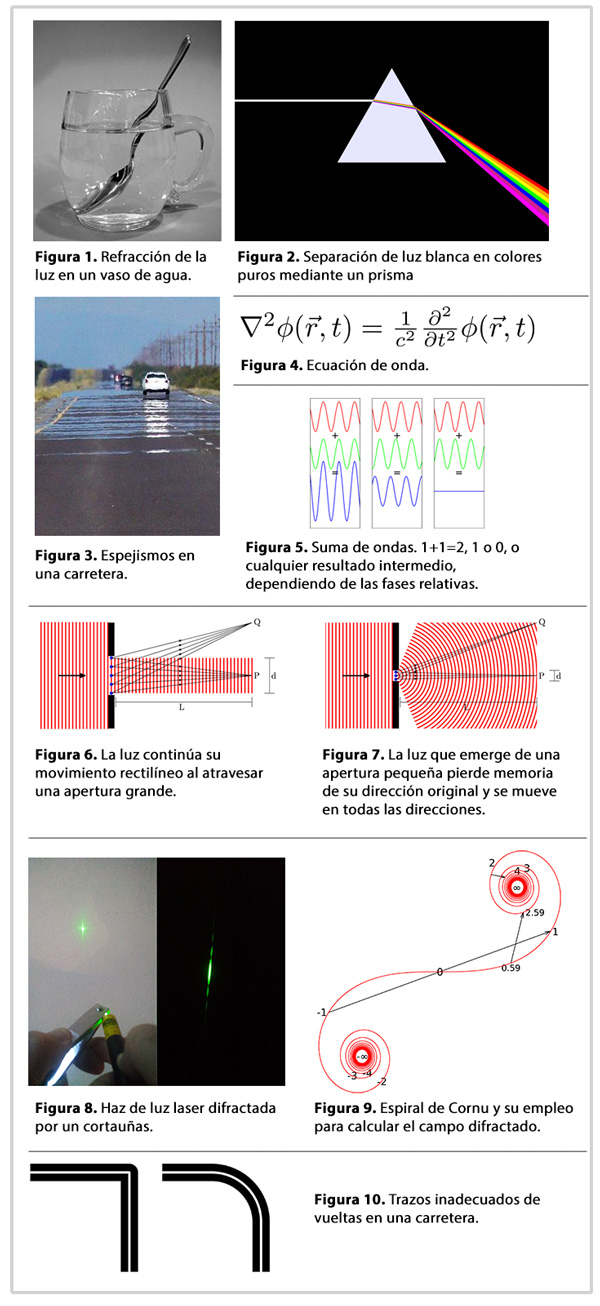
Todos hemos visto cómo cuando introducimos una cuchara en un vaso con agua, ésta parece romperse (ver figura 1). Esto se debe al fenómeno de refracción; la luz cambia su dirección de propagación cuando entra o sale de un medio. Cuánto cambia su dirección depende de la velocidad relativa con que se mueve dentro y fuera del medio. Por ejemplo, en el espacio vacío, la luz viaja 299,792,458 metros, casi trescientos mil kilómetros, cada segundo, mientras que en el aíre viaja 299,709,438 metros cada segundo, velocidad ligeramente menor. La diferencia de velocidades es de 20 metros por segundo, equivalente a la de un automovil moviendose apenas a 72 kilometros cada hora, una insignificancia. Sin embargo, dentro del agua o dentro de una pieza de vidrio transparente, la luz recorre 225,407,863 metros y 199,861,638 metros cada segundo, respectivamente, velocidades significativamente menores que en el espacio vacío. Además de depender de la naturaleza del material que atraviesa (sea aire, agua, vidrio, etc.) la velocidad de la luz depende de la frecuencia con que oscila su campo electromagnético, es decir, de su color. Esto permite que un prisma de vidrio descomponga un haz de luz en múltiples haces de con colores puros, monocromáticos (ver figura 2), cada uno moviéndose en una dirección diferente. Al mapear colores en direcciones, un prisma nos permite medir qué colores absorbe una sustancia o qué colores emite una lámpara y con qué intensidad, el llamado espectro de la sustancia, y a partir de este, identificarla. Este es el principio de la espectroscopía. Tratar de entender los espectros condujo en los inicios del siglo XX a la mecánica cuántica, la cual revolucionó nuestra concepción de la materia.

En los ejemplos anteriores, la luz viaja en líneas rectas por tramos y simplemente cambia su dirección en las interfaces que separan distintos medios, pues en estas interfaces la velocidad de la luz cambia abruptamente. ¿Qué pasaría si el cambio de velocidad fuese suave en vez de abrupto? Considere el pavimento de una carretera. La luz en un día soleado puede calentarlo fuertemente, produciendo a su vez incrementando a su vez la temperatura del aire en la vecindad de la superficie asfaltada. La luz se propaga más rápidamente en el aire caliente cerca del pavimento que en el aire frío algunos metros más arriba, por lo cual se refracta gradualmente siguiendo trayectorias curvas. Así, algunos rayos de luz provenientes del cielo azul, al pasar rasamente sobre la carretera, doblan su trayectoria y llegan a nuestros ojos viajando de abajo hacia arriba, como si se hubieran reflejado en un charco de agua. Este es el origen de los espejismos (ver figura 3).

En este artículo quiero mencionar otra forma, mucho más sutil, en que los rayos de luz se pueden alejar de su movimiento rectilíneo.  Para entenderla, debemos recordar que la luz, así como el sonido y las olas del mar, es una onda. Si en algún lugar del oceano la altura del agua se hallara momentáneamente por arriba de su nivel nominal, el peso adicional asociado tendería a hacerla bajar. Sin embargo, en este proceso, tendría que hacerse de un lugar, para lo cual empujaría al agua a su alrededor, haciendo que suba su nivel. Así, al bajar la altura en un lugar, tendría que subir en un lugar vecino y la altura se propagaría de un lugar a otro en forma de ola, aunque el agua misma se quede esencialmente en su lugar original. Similarmente, si nosotros comprimiéramos cierta masa de aire, la presión adicional provocaría una expansión. Sin embargo, para expanderse tendría que empujar al aire a su alrededor comprimiendolo. Así, la presión se propagaría de un lugar a otro como una onda de sonido aunque el aire se quede alrededor de su posición inicial. De manera análoga, un campo electromagnético en una región del espacio provoca un campo electromagnético en una región vecina, propagándose en forma de una onda electromagnética que no es más que luz visible si su frecuencia de oscilación se halla entre aproximadamente 400 y 800 terahertz (un terahertz significa un millón de millones de oscilaciones cada segundo). Curiosamente, aunque los tres tipos de ondas mencionados arriba son de naturaleza muy distinta, correspondiente a un campo de alturas, un campo de presiones o un campo electromagnético, las tres están aproximadamente descritas por la misma ecuación, la llamada ecuación de onda. Para satisfacer su curiosidad, el lector puede contemplarla en la figura 4.

Uno de los principios para describir cómo se propagan las ondas fue descrito por el físico danés Christiaan Huygens en 1678, ¡antes aún de que se conociera la ecuación de onda!. Su formulación fue perfeccionada por el físico francés Augustin-Jean Fresnel en 1816 y fue justificada matemáticamente por el físico alemán Gustav Kirchhoff en 1883. En escencia, este principio dice que cada punto sobre un frente de onda, por ejemplo, en una cresta de una ola, se comporta como fuente de una onda secundaria que se propaga en todas las direcciones. Elcampo total en una región no es más que la suma de todas las ondas originadas en cada uno de los puntos en la frontera de dicha región. Para entender cómo aplicar este principio debemos aprender a sumar ondas. La figura 5 ilustra las curiosas propiedades de la suma de ondas. Del lado izquierdo sumamos dos ondas idénticas, ilustradas por su crestas y valles. El resultado es una onda cuyas crestas y valles son del doble de altura y de profundidad que las de las ondas que la componen. Al centro de la figura se muestran dos ondas idénticas excepto porque las crestas y valles de una de ellas llegan ligeramente antes que las  de la otra; las dos ondas están ligeramente fuera de fase. En este caso, puede ser que el resultado de la suma tenga crestas y valles de la misma altura que sus componentes. En el extremo derecho se muestran otra vez dos ondas idénticas excepto porque las crestas de una de ellas llegan junto con los valles de la otras y viceversa; las ondas están en antifase. En este caso las crestas de cada onda se anulan con los valles de la otra, dando origen a un campo nulo. Podríamos decir que, curiosamente, al sumar ondas, 1+1=2 a veces, pero otras veces 1+1=1 y otras más 1+1=0. De hecho, 1+1 puede ser cualquier valor entre 0 y 2, dependiendo de la fase relativa entre los sumandos. El valor 2 corresponde a ondas en fase que interfieren constructivamente, mientras que el valor 0 corresponde a ondas en antifase que interfieren destructivamente.

Apliquemos entonces los principios de Huygens, Fresnel y Kirchhoff para estudiar la propagación de una onda que atraviesa una perforación grande en una pantalla opaca. La figura 6 muestra una onda moviéndose hacia la derecha (flecha gruesa) cuyos frentes de onda (líneas rojas) son verticales. Esta onda es bloqueada por una pantalla opaca (líneas negras gruesas) que sólo dejan pasar al campo a través de una apertura grande. Cada punto de los frentes de onda en esta apertura (como los puntos azules) es fuente de ondas secundarias y el campo total es la suma de todas éstas. Si observáramos la luz transmitida a una gran distancia L de la pantalla, las distancias (flechas angostas) desde todos los puntos en la apertura hasta el punto P, colocado en la dirección de la onda original (flecha gruesa), serían prácticamente iguales, mientras que las distancias al punto Q, desviado de la dirección original serían todas distintas. Por lo tanto, en la dirección de P habrá interferencia constructiva y el campo será grande, mientras que en la dirección de Q habrá interferencia destructiva y el campo será pequeño. Casi toda la energía de la onda continuará su movimiento hacia la derecha como si la luz se moviera en línea recta.

Comparemos el caso anterior con la figura  7, correspondiente a una apertura tan pequeña que las distancias desde todos los puntos en la apertura hasta Q son iguales entre sí, como lo son todas las distancias desde la apertura hasta P. En todas las direcciones hay interferencia constructiva y la luz viaja en todas direcciones, como si hubiese olvidado de la dirección original (flecha gruesa) en que se movía. La capacidad de la luz de cambiar su dirección de movimiento al pasar a través de aperturas pequeñas se conoce como difracción.

En la figura 8 muestro el resultado de un experimento muy simple que el lector podría reproducir. Del lado izquierdo se muestra un laser (podría emplearse un apuntador laser como los que se venden en las papelerías) cuya luz ilumina una pared despues de haber pasado a través de la apertura entre las hojas de un cortauñas. Al cerrar lentamente el cortauñas, dicha apertura se hace pequeña. Cuando se vuelve muy pequeña, la manchita luminosa que produce el laser empieza crecer en lugar de disminuir como muestra la línea vertical en la foto. Si los filos del cortauñas se mantienen horizontales, la mancha luminosa se extiende en la dirección vertical, como muestra con mayor claridad la foto del lado derecho, tomada de más cerca que la del lado izquierdo y habiendo obscurecido el cuarto. Además de mostrarse una línea vertical, se observa que la misma es interrumpida por una serie de franjas obscuras. Éstas corresponden a direcciones a lo largo de las cuales hay interferencia destructiva.

Para calcular patrones luminosos tales y como el mostrado del lado derecho de la figura 8 es necesario sumar las contribuciones de todas las ondas secundarias para aperturas de tamaño intermedio entre las  ilustradas en las figuras 6 y 7. Después de una serie de manipulaciones matemáticas, los físicos y los ópticos han encontrado una forma muy simple de hacer dicha suma gráficamente, empleando una figura atractiva conocida como la espiral de Cornu en honor al físico frances Marie Alfred Cornu (ver figura 9) y que se usa siguiendo la siguiente receeta: Si deseamos averiguar cuánto vale el campo óptico en un punto dado detrás de la apertura, debemos medir los ángulos que un rayo de luz debería desviarse para llegar hasta dicho punto pasando por uno y otro extremo de la apertura. Los ángulos serán positivos si la desviación es, digamos, hacia arriba, y negativos si es hacia abajo. Estos ángulos deberán expresarse en radianes en lugar de grados (un radián corresponde a 180/π grados, donde π≅3.14159265359 es el área de un disco de radio 1) y después deberán multiplicarse por la raiz cuadrada de la distancia a la apertura dividida entre la longitud de onda de la luz. Finalmente, deberán multiplicarse por la raiz cuadrada de π para obtener dos números que llamaremos Ay B. A continuación, se miden las distancias A y B sobre la espiral misma a partir de su centro (0) para obtener dos puntos correspondientes. En la figura 9 he marcado algunas de estas distancias, las cuales pueden ser positivas o negativas, dependiendo si los rayos de luz serían desviados hacia uno u otro lado de la apertura. Para terminar, dibujamos una flecha que una los dos puntos así elegidos.  El campo electromagnético es proporcional al tamaño de esta flecha y su energía es proporcional al cuadrado. En la figura muestro algunas de estas flechas. Una de ellas va del punto A=-1 a B=1, otra de A=0.59 a B=2.59 y la última de A=2.1 a B=4.1. Notamos que aunque la diferencia B-A=2 es la misma para estas tres flechas, su tamaño es muy distinto. La primera correspondería a la región más luminosa al centro de la figura 8, mientras que las otras dos corresponderían a la primera y la segunda franja obscura a partir de la zona central.

La espiral de Cornu tiene una propiedad que la vuelve muy importante en disciplinas que no tienen relación alguna con la óptica: su radio de curvatura resulta ser inversamente proporcional a la distancia recorrida desde su centro. Para ilustrar esta propiedad, imagine que Ud. va manejando un automóvil rumbo al norte sobre una carretera de alta velocidad y el camino da vuelta hacia el oeste. Si la vuelta fuese abrupta, como ilustra el lado izquierdo de la figura 10, seguramente Ud. se saldría del camino y tendría un accidente a menos que hiciera un alto casi total justo antes de dar la vuelta. Para evitar este percance, el tramo que va al norte debería unirse con el tramo que va al oeste mediante un tramo curvo suficientemente amplio para que la fuerza centrífuga no arroje al vehículo fuera del camino mientras que su dirección varía suavemente. Una forma simple de lograr esto es mediante un segmento de círculo que sea tangente en sus extremos a los tramos rectos, como ilustra el lado derecho de la figura 10. Esta solución tiene aún un pequeño inconveniente. Cuando un automóvil recorre un segmento recto, su volante de dirección debe tener cierta orientación, mientras que al recorrer un segmento circular, el volante debe tener una orientación distinta. Durante el tiempo que tarda el conductor del vehículo en dar vuelta al volante, el vehículo no sigue una trayectoria recta ni circular. Por lo tanto, el vehículo no puede seguir el trazo exacto de la carretera cuando consiste de fragmentos de rectas y de círculos. En sí, esto no es demasiado problemático si los carriles son tan anchos que permitan a los vehículos alejarse un poco para después regresar a la trayectoria trazada.

El problema se vuelve mucho más serio para un ferrocarril, obligado a seguir exactamente el trazado de los rieles. Al pasar abruptamente de un tramo recto a un tramo circular, la aceleración pasaría abruptamente de a=0  a la aceleración centrípeta  a=v²/R de un movmiento circular uniforme con radio de curvatura R y que se recorre con velocidad v. Esto provoca enormes esfuerzos sobre las vías responsables de desviar al tren de la trayectoria, conduciendo a deformaciones en las vías que subsecuentemente provocarían vibraciones en el tren y posibles descarrilamientos. El mismo tipo de problemas afrontarían las vías del metro, que no es más que un tren urbano de alta velocidad. Para evitar estos esfuerzos abruptos, las normas de construcción de vías férreas especifican que debe haber una curva de transición a la entrada y a la salida de cualquier tramo curvo. Esta curva de transición debe tener la forma de un fragmento de una espiral de Cornu, de manera que tanto la dirección como la curvatura, y por lo tanto, la aceleración centrípeta, varíen suavemente conforme se avanza en el recorrido. Para trenes de alta velocidad, esta transición permite también ajustar suavemente la altura relativa entre ambos lados de la vía, logrando peraltes tales que el centro de fuerzas que actuan sobre los carros del tren siempre caigan sobre el centro de las vías y los pasajeros viajen cómodamente sin ser afectados por aceleraciones laterales.

Este problema ilustra cómo los métodos matemáticos desarrollados para atacar problemas fundamentales en física, como es el problema de la difracción de ondas por aperturas, puede hallar aplicaciones en disciplinas totalmente disímiles en apariencia como es el diseño de carreteras, vías de tren y líneas del metro. De no emplearse estos métodos en el último caso, podrían producirse deformaciones en las vías, vibraciones durante los recorridos y podrían provocarse accidentes.

Artículo publicado originalmente “Difracción de la luz y las vías del metro” en el periódico Unión de Morelos por miembros de la Academia de Ciencias de Morelos A.C.