Desde siempre, el ser humano ha sido bendecido con la curiosidad, es lo que nos hace explorar, experimentar y buscar cada vez más conocimientos.
Uno de los propósitos de este ensayo es que más jóvenes puedan ver las matemáticas desde otro punto de vista. Sin duda alguna, las matemáticas son mi campo favorito de las ciencias, pero al hablar con más jóvenes de mi edad, me enteré que a la mayoría las matemáticas les parecían un poco tediosas y aburridas. Bueno, alguna vez pensé igual que estos jóvenes que mencioné pero una de las cosas que me hizo cambiar de opinión sobre eso, fue el adentrarme en un tema específico de matemáticas y notar que en realidad tiene muchas aplicaciones, que de simples fórmulas se puedan resolver bastantes problemas. Creo que si no fuera porque un día me puse a investigar a fondo un tema jamás les habría agarrado gusto a las matemáticas. Es por eso que mi tema para este ensayo es el triángulo de Pascal, porque sin duda, es uno de los temas más impresionantes debido a sus múltiples aplicaciones. En mi opinión, entre más extenso sea un tema, es más interesante, descubres más, y te das cuenta de lo impresionante que pueden ser las cosas si te ánimas a querer descubrirlas.
Quiero empezar la introducción a mi tema con una definición del triángulo de Pascal, puede definirse como un conjunto de números infinito en forma simétrica de triángulo que expresan coeficientes binomiales. Pero claro, este triángulo nos sirve para mucho más que solo eso.
Historia.
Empecemos por los antecedentes históricos. El triángulo de Pascal es llamado así por la persona a quien se le atribuyen la mayoría de sus aplicaciones actualmente conocidas, si, hablo de Blaise Pascal, pero no todo el mundo está de acuerdo en atribuirle todo el crédito a Blaise.
Los persas se lo atribuyen a Omar Khayyám, es por eso que en Irán se le llama “El triángulo de Khayyám”. En China se lo atribuyen a Yang Hui y le llaman “El triángulo de Yang Hui”. En Italia creen que es creación de Niccolo Fontana Tartaglia, y es conocido como “Triángulo de Tartaglia”
Pero aquí lo conocemos como triángulo de Pascal en nombre de Blaise Pascal, quien lo mencionó en “Triaité du trianglemarithmétique (Tratado del triángulo aritmético) publicado en 1654. Incluso, llegó a ser conocida la historia de que el triángulo fue creación de uno de los alumnos de Pascal y que Blaiselo publicó como suyo.
Independientemente de quién lo haya creado, el caso es que actualmente contamos con él y que puede ser de gran utilidad en muchas cosas. Claro nunca está de más el saber de dónde provienen las cosas o quién las creó, pero me parece que es mucho más importante saber cómo funcionan esas creaciones y cómo aplicarlas.
Si bien la mayoría de la gente sabe del triángulo de Pascal por los coeficientes binomiales, al estudiarlo más nos damos cuenta que es todo un estuche de monerías matemáticas que a continuación conoceremos.
Construyendo la pirámide.
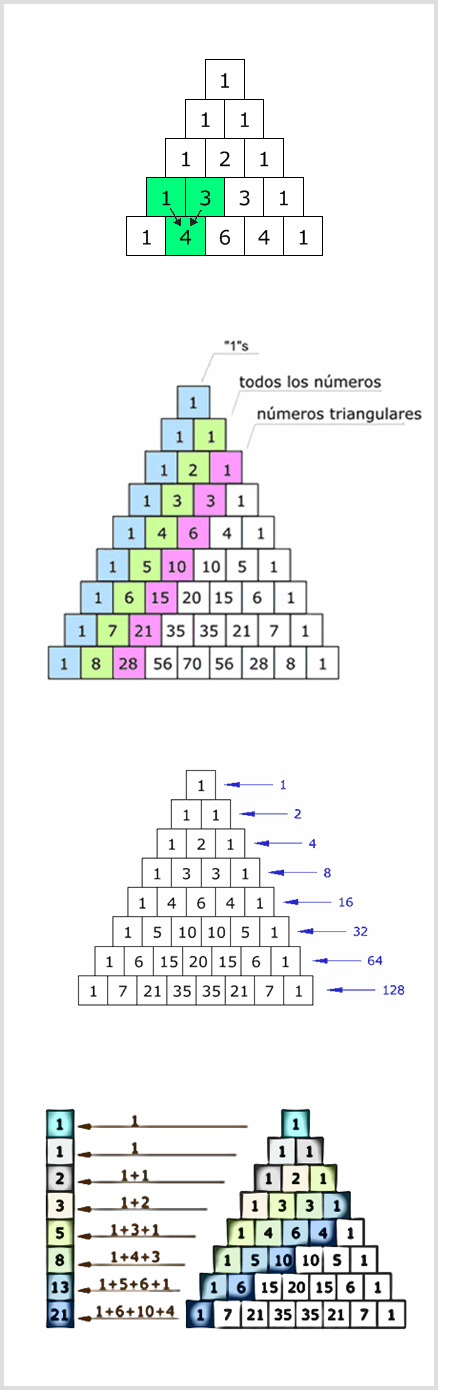
Para empezar, debemos armar el triángulo de la siguiente manera. Se comienza con un número uno hasta arriba de la pirámide, luego se colocan otros dos unos debajo del primero de forma triangular.
Ahora, se comienzan a sumar de dos en dos los números, anotando el resultado debajo de ellos, y así consecutivamente con el resto de los números. Todos los números son el resultado de la suma de los dos de arriba y lo extremos siempre van a ser uno. Las líneas se cuentas de arriba hacia abajo, la primera línea es la línea cero, y desde la segundo se comienza a contar. Una vez armado, podemos analizarlo.
Como se puede notar, es bastante fácil construir el triángulo de Pascal, igual de fácil es saber cómo utilizarlo, la parte difícil se la llevó el creador del triángulo, por el simple hecho de crearlo. Pero, gracias a él ahora nosotros podemos disfrutar de sus aportaciones.
Resulta bastante impresionante cómo de una simple pirámide tan fácil de armar pueden salir tantas aplicaciones, y aún más impresionante imaginar de qué manera a alguien se le pudo ocurrir esta pirámide, sin duda es un producto de la curiosidad del humano para aprender y crear cosas nuevas. Puesto que esa curiosidad por lo nuevo es la que nos impulsa a avanzar, a investigar, a crear, a ser más.
Pautas por default.
Comenzando por las más simples pero no por eso menos interesantes propiedades del triángulo, mencionaré las pautas que lleva el triángulo “por default”, osea sin que apliquemos algún método o fórmula para notarlas.
Números naturales.
Primero veremos la pauta más simple, al lado izquierdo de la pirámide está la diagonal de los unos, justo un lugar a la derecha está la pauta en diagonal de los números naturales, que son todos los número que nos enseñan desde jardín de niños.
Números triángulares.
Justo al lado derecho de la pauta en diagonal de los números naturales está la pauta en diagonal de los números triángulares, los números triángulares son todos aquellos números con lo que se puede formar una pirámide, cómo el 3, el 6, el 10, etc. Y todos estos números los podemos encontrar en el triángulo de Pascal a un lado de los números naturales.
Números tetraédicos.
Debajo de los números triángulares, está la pauta de los números tetraédicos. Los número tetraédicos son los que representan una figura con su base y tres lados llamada tetraedo. El enésimo número tetraédico es la suma de los primeros n números triángulares. Y siguen la secuencia: 1, 4, 10, 20, 35, etc.
Números primos.También podemos observar de estre triángulo que si el primer número de una fila es un número primo, el resto de los integrantes de la fila serán divisibles entre él, exeptuando al uno. Por ejemplo, el 11, en su línea están el 11, 55, 16, 330, 462, 462, 330, 165, 55, 11 y todos ellos, son divisibles entre 11.
Bueno, hemos empezado a conocer el triángulo por sus atributos más simples, sus pautas “por default”, pero creanme, es solo el inicio de un tema que en mi opinión es sumamente interesante y profundo.
Mas curiosidades sobre el triángulo de Pascal.
Espejito, espejito.
No es un brillante descubrimiento que el triángulo de Pascal sea totalmente simétrico. Quizá no sea tan impactante, pero es solo una más de las numerosas características de este triángulo.
De dos en dos.
Hay muchas cosas que podemos sacar de este triángulo, una de ellas son las potencias de dos, a las cuales podemos llegar al sumar todos los números de un nivel en el triángulo. Por ejemplo, si sumamos el primer nivel nos queda algo así: 1+1=2, luego el segundo nivel: 1+2+1=4, tercer nivel: 1+3+3+1=8 y el cuarto nivel: 1+4+6+4+1=16. Después de sumar varias veces los niveles nos damos cuenta de que son las potencias de dos.
Aplicando la de Fibonacci.
Muy bien, ya vimos algunas cosas que el triángulo tiene, como simetría, las potencias de dos, algunas pautas, ahora veremos algo un poco más impresionante.
La sucesión de Fibonacci es realmente interesante, se crea a partir de dos números unos, se suman entre ellos y dan un tercer número, la sucesión continua sumando los dos últimos números de la sucesión dando una sucesión así: 1, 1, 2, 3, 5, 8, 13, 21…
Ahora bien, en el triángulo de Pascal también podemos ver esta sucesión. Primero, tenemos que ubicarnos en un uno de la diagonal de los unos en la izquierda. Damos un paso hacía arriba, uno a la derecha y sumamos, otro paso hacía arriba, otro hacía la derecha y sumamos. Si repetimos las operaciones hasta llegar al tope de la pirámide y anotamos los resultados en forma de lista descendente, el triángulo nos sorprenderá una vez más, nos daremos cuanta de que tenemos ahí escrita la sucesión de Fibonacci.
Pares, impares y un tal Sierpinski.
Waclaw Sierpinski (1882-1969) fue un matemático polaco que en 1919 creo el llamado “triángulo de Sierpinski” que entre otras cosas, demostraba que era posible hacer una curva que se cruzara consigo misma en todos sus puntos. El triángulo es un fractal, un fractal es un objeto cuya estructura básica de repite en diferentes escalas.
Lo curioso de este triángulo, es que tiene una relación muy interesante con el triángulo de Pascal. Si al triangulo de Pascal le hacemos una modificación coloreando todos los números pares de un color y los impares de otro conseguiremos un triángulo muy parecido al del señor Sierpinski.
Quizá una buena pregunta sería el cómo el trabajo tan elaborado de dos personas que ni siquiera se conocieron pueden concordar tanto, pues mi respuesta sería que eso es lo que hace tan interesantes a las matemáticas, que valdría la pena que lo averiguaras.
Haciendo magia con Blaise Pascal.
Ya vimos bastante sobre las características de este triángulo, pero empecemos a ver cómo podemos aplicarlo a casos reales, no sirve de nada saber métodos sin saber como aplicarlos, y este triángulo como muchas otras cosas de las matemáticas tiene varias aplicaciones.
De regreso a la escuela.
Como ya había mencionado, el triángulo de Pascal es conocido por el binomio de Newton, o sea para conocer los coeficientes de la expansión de un binomio.
Por ejemplo la expansión binomial de (x +1)2 es 1x2 + 2x + 1, números que podemos ver en las primeras líneas de la pirámide, 1, 2,1.
La expansión binomial de (x+1)3 es 1x3 + 3x2 +3x +1, que está en la siguiente línea de la pirámide, 1, 3, 3, 1. Y si seguimos aumentando la potencia de uno en uno, el patrón se seguiría repitiendo.
Quizá hayan recordado este tema, ya que al parecer es de las pocas cosas que se mencionan sobre el triángulo de Pascal en las escuelas a nivel medio superior. Pero, ¿no creen que sería genial el que enseñarán no solo este tema sino lo más profundo que se pueda acerca de este triángulo? Si en el plan de estudios no se considera esto, me parece que nos toca a nosotros los estudiantes investigar, pensar, buscar y aprender más por nuestra cuenta, ya que es la tarea del ser humano saber más acerca de su entorno. Se los dejo a su criterio.
Águila o sol.
Una de las aplicaciones del triángulo es ver probabilidades de combinaciones, por ejemplo si te dan un determinado número que represente las veces que lanzas una moneda, el triángulo de Pascal te da las probabilidades de que caiga águila o sol.
Siguiendo el ejemplo de la moneda veremos cuántas posibilidades hay cuando lanzamos cinco veces una moneda.
Primero, hay solo una posibilidad de que nos salgan cinco águilas (A-A-A-A-A). Hay cinco posibilidades de que nos salgan cuatro águilas y un sol (A-A-A-A-S), (A-A-A-S-A), (A-A-S-A-A), (A-S-A-A-A), (S-A-A-A-A). Hay diez posibilidades de que nos salgan tres águilas y dos soles (A-A-A-S-S), (A-A-S-S-A), (A-S-S-A-A), (S-S-A-A-A), (S-A-A-A-S), (S-A-A-S-A), (S-A-S-A-A), (A-S-A-A-S), (A-S-A-S-A), (A-A-S-A-S). Hay diez posibilidades de que nos salgan dos águilas y tres soles (S-S-S-A-A), (S-S-A-A-S), (S-A-A-S-S), (A-A-S-S-S), (A-S-S-S-A), (A-S-S-A-S), (A-S-A-S-S), (S-A-S-S-A), (S-A-S-A-S), (S-S-A-S-A). Haycinco posibilidades de que nos salgan cuatro soles y una águila (S-S-S-S-A), (S-S-S-A-S), (S-S-A-S-S), (S-A-S-S-S), (A-S-S-S-S). Y por último, hay unaúnica posibilidad de que nos salgan cinco soles (S-S-S-S-S). Si ponemos atención al patrón de las posibilidades, nos podemos dar cuenta que son los mismos números que hay en la línea con el número de lanzamientos, en este caso fueron cinco lanzamientos, y si vemos la línea número cinco, estará el patrón de posibilidades (1-5-10-10-5-1).
Me parece que esto da un motivo más para decir que vale la pena estudiar este triángulo y muchos temas de matemáticas más. Son simplemente sorprendentes las cosas que puede esconder un triángulo.
Combinaciones
La propiedad en mi opinión más curiosa del triángulo de Pascal es las de las combinaciones, y para explicarlas pondré un ejemplo.
Supongamos que tenemos 24 canicas dentro de una cesta, si metemos la mano a la cesta con los ojos cerrados y sacamos solamente cinco canicas. ¿Cuántas combinaciones diferentes pueden salir en esas cinco canicas?
Bien, pues la respuesta quizá requeriría el uso de un método muy tardado, sin embargo, gracias al triángulo de Pascal, podemos conocer la respuesta muy fácilmente. Solo tenemos que tomar el número de canicas que hay en la cesta, que en este caso son 24 y nos posicionamos en esa línea, en la línea 24 del triángulo, después tomamos la segunda variable que en este caso son las 5 canicas que agarramos de la cesta y ya posicionados en la línea 24, nos movemos 5 lugares a la derecha. Y ahí está la respuesta: 42504.
Es impresionante, pero es cierto. Con esta propiedad del triángulo a mi parecer se puede ver perfectamente los frutos de tanta investigación y trabajo en el triángulo, es un claro ejemplo de que las matemáticas, el esfuerzo y la dedicación sirven de bastante, nos ahorramos mucho procedimiento para llegar a la respuesta y tan solo es una de tantas propiedades del triángulo.
El quincunce
El quincunce es una máquina creada por Sir Francis Galton que consta de varios cilindros o palos ordenados en forma de triángulo de Pascal sobre una superficie totalmente vertical.
En la cima o punto más alto de la pirámide se dejan caer pelotas, que viajan entre los palos hacia abajo y caen en contenedores previamente puestos debajo del quincunce. A simple vista es un método para poner las pelotas de manera totalmente aleatoria dentro de los contenedores, pero si observamos detenidamente, impresionantemente nos daremos cuenta que caen con un patrón, la distribución normal.
La distribución normal se le llama a una distribución de variable aleatoria continua que a partir de un parámetro específico se convierte en una gráfica simétrica.
Lograr la simetría en una distribución aparentemente aleatoria no es tarea fácil, es realmente increíble que nuevamente aplicando el triángulo de Pascal se pueda lograr.
Cerrando el triángulo
Siendo sincera, una de las cosas que me motivaron a hacer este ensayo fue que otros jóvenes lo pudieran leer y notaran que el saber matemáticas no solo es para los que les obsesiona ir bien en la escuela o para gente aburrida, antes de hacer este ensayo, yo misma no sabía todo esto sobre el triángulo de Pascal, y estoy segura de que aún me falta mucho por conocer acerca de él, pero si algo es cierto es que me impresioné demasiado al ver la profundidad que tiene y pensé que deben haber mil temas más de matemáticas con muchas aplicaciones que desconozco y estoy convencida que vale la pena aprenderlos. Mientras escribía todo esto, traté de enfatizar lo más que pude la extensión de este tema y aún mejor, la extensión de sus aplicaciones.
Me gustaría que el tema del triángulo de Pascal se diera en todas las preparatorias y escuelas de este nivel escolar, como un tema para profundizar. Pero por ahora me conformaría con que este texto anime a otros a estudiar temas por ellos mismos, sin esperar que se los enseñen en la escuela, y no solo de matemáticas. Aún hay muchas cosas por descubrir.
Si alguien no hubiera tenido el interés de estudiar, crear algo nuevo, quizá no contáramos con muchas cosas que tenemos hoy en día. El mundo está lleno de cosas nuevas por descubrir, solo hay que salir a encontrarlas.
Artículo publicado originalmente “Triángulo de Pascal” en el periódico Unión de Morelos por miembros de la Academia de Ciencias de Morelos A.C.
Cómo citar: Autor, C., Karen Hernández Montes Colegio de Bachilleres del Estado de Morelos Ganadora del Premio ACMor-La Unión de Morelos al ensayo científico juvenil. (2018, 21 de Septiembre ) Triángulo de Pascal. Conogasi, Conocimiento para la vida. Fecha de consulta: Octubre 9, 2025
Esta obra está disponible bajo una licencia de Creative Commons Reconocimiento-No Comercial Compartir Igual 4.0




Deja un comentario
4 Comentarios en "Triángulo de Pascal"
Falta decir que son números de la potencia de 11, 11^0=1, 11^1=11, 11^2=121, etc…
Pero por el resto, muy buen ensayo
GRACIAS!!