El Espectro Electromagnético es Propiedad de la Nación: Parte III

-Pun chis pun chis pun chis pun pun / pun chis pun chis pun chis pun pun…

-¿Qué disparate estás diciendo?

-Nada, sólo repito un ritmo que venía escuchando.

-¡No es posible que quieras repetir ese ritmo!

-En gustos se rompen géneros.

-Pero no tiene casi nada de información.

-La música es abstracta, no tiene por qué tener significado.

-No me refiero a su significado, sino a la cantidad de información. Si escuchas un pequeño fragmento, es como si lo hubieras escuchado todo. De hecho, toda la pieza se puede especificar como pun chis tres veces, pun dos veces y vuelves a empezar. Una computadora podría repetirlo hasta el aburrimiento; no tiene ni requiere talento ni trabajo humano.

-Ya, ya. ¿Y conoces algo mejor?

-Considera el ritmo Dha ghe te re ki ta dha / dha ghe te re ki ta dha / dha ghe te re ki ta /dha – dha – dha – / dha ghe te re ki ta.

–¿Y eso?

-Es un ritmo  proveniente de la India para intepretarse en tabla, una especie de pequeño tambor; cada sílaba representa un golpe distinto en una parte específica de la tabla, produciendo sonidos característicos. La complejidadde este ritmo es mucho mayor que la de tu punchis punchis.

-Pues no parece muy difícil.

-Complejidad no es dificultad. Una secuencia es más compleja mientras más larga sea su descripción. Intenta hacer una descripción lo más corta posible de mi ritmo y compárala con mi descripción del tuyo (el lector puede intentar hacer este ejercicio). Si además el músico que la interpreta es creativo, hará cambios inesperados durante su ejecución que te sorprenderán. Una secuencia tiene más información y es más rica mientras más impredecible sea.

-No acabo de entender.

-Déjame darte otro ejemplo. Imagina que prendes la radio y escuchas que la oposición acusa al gobernante de tramposo, que los organismos fiscalizadores no hacen nada al respecto y, finalmente, que gracias al gobierno serás feliz. ¿Qué habrás aprendido?

-Nada. Eso dicen todo el tiempo todos los días.

-En cambio, imagínate escuchar que la oposición felicita al gobernante por su honestidad, que el organismo fiscalizador castiga al gobernante por tramposo o que el gobernante confiesa errores que obscurecen tu futuro.

-Eso es imposible, aquí no puede pasar.

-Eso es improbable, pero en principio, podría pasar. Noticias inesperadas como esas te sorprenderían, te dirían algo que no hubieras esperado, te darían información (aún si esa información fuese falsa). La información es una medida de la improbabilidad; es algo así como la entropía, pero al revés.

-¿Entropía?

-Es un concepto que tiene que ver con la termodinámica, una medida del desorden. Conforme un sistema cerrado evoluciona, su estado se vuelve cada vez más probable, su entropía aumenta. Esta es la segunda ley de la termodinámica.

-¿Y cómo se mide la información?

-Déjame contestarte con una pregunta. Voy a pensar en un dígito cualquiera, un número entre 0 y 9. Cuando te lo diga ¿cuánta información te habré dado?

-No sé.

-Bueno, no importa, pero considera que ahora pienso dos o tres dígitos. ¿Cuánta información te habré dado cuando te los diga?

-Tampoco sé, pero segúramente será dos o tres veces más que cuando me hubieras dicho sólo un dígito.

-Exacto. Si cada dígito es independiente de los anteriores, la información que te proporciona cada uno es la misma y la información total es la suma de la información que te da cada parte. La información que te proporcionan mensajes independientes es aditiva. Ahora déjame preguntarte, ¿cuántos números distintos podrías escribir con uno, dos o tres dígitos?

-Diez, cien o mil, respectivamente.

-Y ¿conoces alguna función matemática cuyo valor sea dos o tres veces mayor cuando se aplica a cien o a mil que cuando se aplica a diez?

-Claro, el logaritmo.

-Así es, el logaritmo base diez de 10 es 1, el de 100 es 2 y el de 1000 es 3. La probabilidad de adivinar un número específico de un dígito es 1/10, si es de dos dígitos es 1/100 y para tres dígitos es 1/1000. Eso sugiere definir la cantidad de información de un mensaje como el logaritmo del inverso de su probabilidad.

-Pero hay distintos tipos de logaritmos. Hay logaritmos base 10 o logaritmos naturales…

-Eso no importa mucho, pues al cambiar de base los logaritmos simplemente se ven multiplicados por una constante. Lo más común es usar la base 2, en cuyo caso, la información se expresa en bits. El número de bits de una secuencia resulta ser igual al número de dígitos binarios (ceros y unos) que se requieren para representarla.

-Y ¿para qué sirve medir la información si no nos fijamos en su significado?

-Al abstraernos del significado podemos contestar preguntas como cuánta información podemos transmitir a través de un canal de información. Por ejemplo, Claude Shannon y Ralph Hartley demostraron durante la primera mitad del siglo XX que la capacidad C de un canal de información es el producto de su ancho de banda B multiplicado por el logaritmo de  la potencia de la señal S sumada a la potencia del ruido R dividida entre R, i.e.,C=B log((S+R)/R), y Shannon demostró que codificando los mensajes adecuadamente se pueden enviar hasta C bits por segundo de forma perfecta,sin cometer error alguno, ¡a pesar de que el canal sea ruidoso! Este tipo de resultados son los que estudian la teoría de la información.

-Explícate.

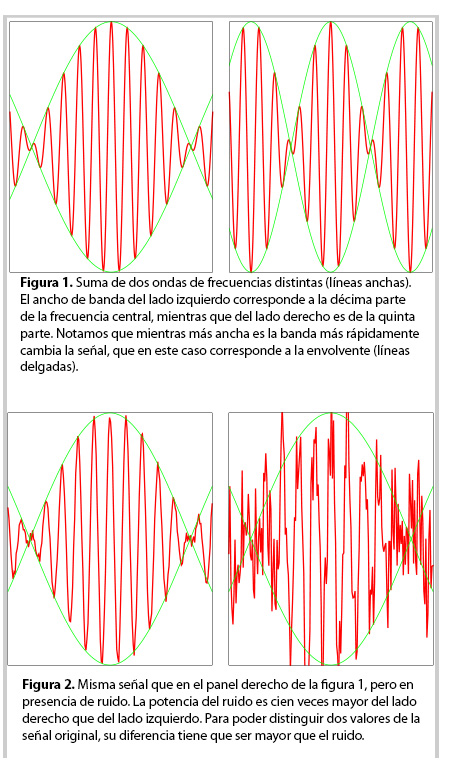
-Como debes saber, solemos transmitir información a través de ondas electromagnéticas [ver referencia 2]. El espectro electromagnético se divide en numerosos canales de radio, televisión, telefonía u otros. Cada canal incluye ondas con muchas frecuencias que forman una banda [ver referencia 3]. Para que estos canales no interfieran entre sí, cada banda tiene asignada una frecuencia central y un ancho de banda que no puede ser demasiado grande pues no debe translaparse con las bandas de frecuencias vecinas. El teorema de Shannon-Hartley mencionado arriba nos dice que la cantidad de información que podemos transmitir cada segundo por un canal crece en proporción a su ancho de banda. Un ancho de banda mayor nos permite cambiar más rápidamente al campo electromagnético y por ende enviar más información por unidad de tiempo (ver figura 1).

-¿Y el ruido?

-Además de la antena de nuestra radiotransmisora, hay muchas otras fuentes de campo electromagnético, incluyendo otras radiotransmisoras lejanas, tormentas en el sol, fluctuaciones en la ionósfera, que es una de las capas altas de nuestra atmósfera, y hasta las rotaciones desordenadas de las moléculas agitadas térmicamente, entre otras. El campo que producen se suma y deforma al campo que nos interesa. Para poder distinguir dos valores del campo, i.e., dos símbolos del alfabeto con que escribimos nuestro mensaje, éstos tienen que diferir entre sí en una cantidad mayor al ruido, lo cual limita el número total de posibles símbolos que podríamos reconocer (ver figura 2). Si la cantidad de ruido fuese enorme, la capacidad del canal sería nula, mientras que si el ruido igualara a la señal, el número de bits que podemos transmitir por segundo sería igual al ancho de banda.

-Recuerdo haber escuchado sobre canales y bandas recientemente en las noticias, cuando han hablado de la nueva ley de telecomunicaciones y el apagón analógico que viene.

-Efectivamente, el teorema de Shannon  nos dice cuánta información podríamos transmitir por un canal si la codificáramos óptimamente. Sin embargo, en las comunicaciones analógicas empleamos códigos muy simples. Por ejemplo, en la radio AM cada valor de la envolvente de la onda electromagnética representa la presión instantánea de una onda de sonido. Si el sonido se repite, como en el “punchis punchis” con que iniciamos esta conversación, esta modulación electromagnética tendría que repetirse una y otra vez, agotando el ancho de banda de la estación sin tomar en cuenta que dicha secuencia no contiene casi nada de información. Si en cambio digitalizáramos dicha información y la codificáramos óptimamente empleando una computadora, bastaría enviar el mensaje “va un punchis punchis” para que el receptor pueda repitir la secuencia sin usar más el ancho de banda, el cual podría emplearse para transmitir información más interesante. Para transmitir una escena en la televisión se envía una señal proporcional a la intensidad de cada punto luminoso (y otras señales relacionadas con su color y el audio) 30 veces por segundo empleando un ancho de banda de seis millones de Hertz (oscilaciones por segundo), aún cuando lo que se transmita sea la imagen de un paisaje que no cambia, desperdiciando así la capacidad del canal en enviar millones y millones de bits redundantes. En cambio, los sistemas digitales tienen una computadora que comprime la información al codificarla antes de enviarla y otra computadora dentro del radio o televisión que la decodifica y expande después de recibirla, disminuyendo fuertemente el ancho de banda requerido del canal de comunicación. Esta compresión/decompresión es análoga a la tecnología que te permite aumentar la capacidad de tus CDs aproximadamente 10 veces cuando copias música empleando el formato digital MP3. De esta manera, hacer la transición digital, conocida como el apagón analógico tiene efectos equivalentes a aumentar 10 veces la capacidad de cada uno de los actuales canales de radio y de televisión.

-Y ¿qué va a pasar con el ancho de banda que va a sobrar? ¿Habrá más canales de televisión? ¿Habrá canales con mejor calidad de imagen? ¿Se usarán para otros propósitos, como por ejemplo, ofrecer internet de alta velocidad a la población?

-Eso… mejor pregúntaselo a tus representantes en las cámaras legislativas.

Artículo publicado originalmente “El Espectro Electromagnético es Propiedad de la Nación: Parte III” en el periódico Unión de Morelos por miembros de la Academia de Ciencias de Morelos A.C.