Algoritmos genéticos

Un algoritmo es una serie de pasos organizados que describe el proceso que se debe seguir, para dar solución a un problema específico. Un algoritmo genético (o AG para abreviar) es una técnica de programación inspirada en la reproducción de los seres vivos y que imita a la evolución biológica como estrategia para resolver problemas de optimización. En general, los algoritmos genéticos (AGs) son parte de la llamada inteligencia artificial; es decir, la resolución de problemas mediante el uso de programas de computación que imitan el funcionamiento de la inteligencia natural.

Los AGs fueron delineados por un par de científicos norte-americanos, John Holland [1929–] en los años 1970 y presentados en 1989 por David Goldberg [1953–] como un método de optimización de búsqueda global, debido a que este tipo de métodos explora todo el espacio de soluciones del problema permitiendo salir de posibles óptimos locales e ir en busca de óptimos globales. Para entender lo que es la optimización hay que considerar que la programación matemática intenta resolver procesos que tienen diferentes posibles soluciones, pero sólo una de ellas corresponde al óptimo global, es decir la solución que se ajusta mejor a las condiciones del mismo problema. Cualquier otra solución que se parezca al óptimo global es un óptimo local.

Los AGs hacen evolucionar una población de individuos, o conjunto de soluciones posibles del problema, sometiéndola a acciones aleatorias semejantes a las que actúan en la evolución biológica tales como mutaciones y recombinaciones genéticas; así como también a una selección de acuerdo con algún criterio, en función del cual se decide cuáles son los individuos más adaptados, que sobreviven, y cuáles los menos aptos, que son descartados.

Un AG funciona de la siguiente manera. Dado un problema específico de optimización a resolver, el AG requiere de un conjunto inicial de soluciones potenciales a ese problema, codificadas de alguna manera y de una función de aptitud que permite evaluar cuantitativamente a cada candidata a solución. Estas candidatas se suelen generar aleatoriamente, o bien pueden ser soluciones que ya se sabe que funcionan, con el objetivo de que el AG depure las opciones válidas hasta escoger la mejor.

Cada una de las soluciones potenciales es evaluada por la función de aptitud, una ecuación matemática, que le da una calificación para saber qué tan “buena” es con respecto a las demás soluciones. Por supuesto, la mayoría de estas soluciones no funcionarán en absoluto, y serán eliminadas. Sin embargo, por puro azar, unas pocas pueden ser prometedoras, es decir, pueden mostrar parte de la solución, aunque ésta sea débil e imperfecta, hacia la solución final del problema. Por lo tanto un AG es un método de búsqueda dirigida basada en probabilidades.

Las candidatas prometedoras se conservan y se les permite reproducirse. Se realizan múltiples copias de ellas, que como no son perfectas a algunas de ellas se les introduce, con cierta probabilidad, cambios aleatorios o mutaciones durante el proceso de copia para garantizar que ninguna solución tenga una probabilidad nula de ser examinada. Luego, esta descendencia digital prosigue con la siguiente generación, formando un nuevo acervo de soluciones candidatas que son sometidas a una ronda de evaluación de aptitud. Las candidatas que han empeorado, o no han mejorado, con los cambios en su código son eliminadas de nuevo; pero, por puro azar, las variaciones aleatorias introducidas en la población pueden haber mejorado a algunos individuos, convirtiéndolos en mejores soluciones del problema, más completas o más eficientes. De nuevo, se seleccionan y copian estos individuos vencedores hacia la siguiente generación con cambios aleatorios, y el proceso se repite. Las expectativas son que la aptitud media de la población se incrementará en cada ronda y, por tanto, repitiendo este proceso cientos o miles de rondas, pueden descubrirse soluciones muy buenas del problema.

En resumen, un AG consiste de los siguientes pasos. Inicialización: se genera aleatoriamente una población inicial constituida por posibles soluciones del problema, también llamados individuos. Evaluación: aplicación de la función de evaluación a cada uno de los individuos. Evolución: aplicación de operadores genéticos (como son selección, reproducción y mutación). Y término: el AG deberá detenerse cuando se alcance la solución óptima, pero ésta generalmente se desconoce, por lo que se utilizan varios criterios de detención.

Los AG requieren que, durante la inicialización, cada uno de los individuos sea codificado en un cromosoma. Cada cromosoma tiene varios genes, que corresponden a cada uno de los parámetros del problema. Para poder trabajar con estos genes en la computadora, es necesario codificar loscromosomas en una cadena, es decir, una serie de símbolos (números o letras). Las formas más empleadas para codificar un cromosoma son: la codificación binaria, codificación de valores finitos, uso de números enteros y uso de números reales. La elección de la codificación dependerá del problema a resolver, así que es preciso estudiar la codificación más óptima según el caso que se esté estudiando; porque la mayoría de las veces, una codificación correcta es la clave de una buena resolución del problema.

Para ilustrar de manera muy simple el proceso de codificación podemos emplear la codificación binaria. Consideremos que uno de los individuos tiene un valor de x = 11. En la codificación binaria sabemos que su cromosoma es (0,1,0,1,1). ¿Cómo sabemos esto? Muy sencillo, si se multiplica el último gen (un 1) por 1, el penúltimo (un 1) por 2, el anterior (un 0) por 4, el segundo (un 1) por 8 y el primero (un 0) por 16 y a continuación se hace la suma, el resultado es 11. De la misma manera se observa que (0,0,0,0,0) equivale a x = 0 y que (1,1,1,1,1) equivale a 31. Esta forma de codificación es la empleada para ilustrar las operaciones de cruzamiento y mutación que se describirán más abajo.

El tamaño de la población debe ser lo suficientemente grande como para garantizar que exista una diversidad en las soluciones y para tener una representación de la mayor parte de la población posible.

El proceso de evolución tiene como fin único el mejorar la población de soluciones mediante la aplicación repetitiva de las operaciones de cruzamiento, mutación y selección. Siguiendo el ejemplo de la naturaleza la diversidad genética está presente en las mutaciones y la reproducción sexual.

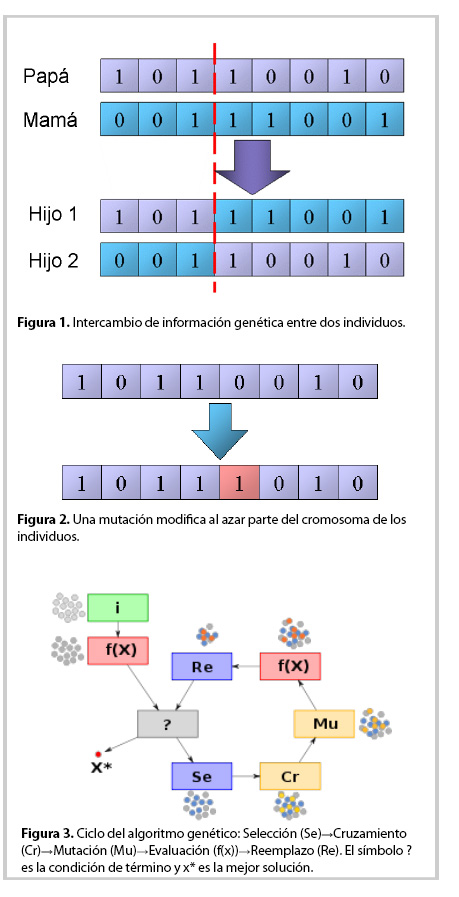
El cruzamiento, o reproducción, es sinónimo de apareamiento entre dos individuos de diferente sexo. Así, en un AG se debe escoger a una pareja de individuos que cruzarán sus cromosomas para generar dos descendientes donde se combinan las características de ambos cromosomas padres. La selección de los individuos que funcionarán como padres puede ser aleatoria o permitiendo que al menos uno de los padres pertenezca al grupo de mejores individuos, tal como se lleva a cabo en la naturaleza donde los cromosomas del individuo más fuerte o mejor adaptado son transferidos a su descendencia. El intercambio de la información genética del par de individuos también se puede llevar a cabo de diferentes formas. Una de ellas se ilustra en la Figura 1, donde aleatoriamente se ha seleccionado un punto de corte común a ambos padres, y que sirve como referencia para intercambiar su información genética para producir dos hijos con características diferentes a los padres, aunque éstos hereden parte de su información genética.

En la evolución una mutación es un suceso bastante poco común, sucede aproximadamente una en cada mil apareamientos. En la mayoría de los casos las mutaciones son letales o no tienen sentido, pero en promedio, contribuyen a la diversidad genética. En un AG tendrán el mismo papel y la misma frecuencia. Una vez establecida la frecuencia de mutación (muy baja), se genera un número entre 0 y 1 de manera aleatoria y si ese número es menor que la frecuencia de mutación se permite que un gen del cromosoma cambie su información; si no, se dejará como está. La mutación modifica al azar parte del cromosoma de los individuos (ver Figura 2), y permite alcanzar zonas del espacio de búsqueda que no estaban cubiertas por los individuos de la población actual.

Finalmente una vez aplicados los operadores genéticos, se seleccionan los mejores individuos para conformar la población de la generación siguiente. Este proceso se realiza por medio de la evaluación de cada individuo con la función de aptitud y se reemplaza la población original.

El AG se deberá detener cuando se alcance la solución óptima, por lo general ésta se desconoce, así que se deben utilizar otros criterios de detención. Normalmente se usan dos criterios: 1) correr el AG un número máximo de iteraciones (generaciones), y 2) detenerlo cuando no haya cambios en la población. Mientras no se cumpla la condición de término se repite el ciclo: Selección (Se) → Cruzamiento (Cr) → Mutación (Mu) → Evaluación (f(x)) → Reemplazo (Re). Ver Figura 3, donde (?) es la condición de término y x* es la mejor solución.

Aunque a algunos les puede parecer asombroso y antiintuitivo, los AGs han demostrado ser una estrategia enormemente poderosa y exitosa para resolver problemas, demostrando de manera espectacular el poder de los principios evolutivos. Se han utilizado algoritmos genéticos en una amplia variedad de campos para desarrollar soluciones a problemas tan difíciles o más difíciles que los abordados por los diseñadores humanos. Además, las soluciones que consiguen son a menudo más eficientes, más elegantes o más complejas que nada que un ingeniero humano produciría.

El éxito actual de los AGs es tal que los Laboratorios de Investigación Naval de los EUA mantiene un programa de investigación aplicada orientada a resolver problemas críticos de ese sector militar (http://www.nrl.navy.mil/aic/) empleando esta técnica de optimización. Este interés también se ha visto reflejado en nuestro país dentro de los Laboratorios Nacionales de Informática Avanzada (http://www.lania.mx) y en la publicación de varios trabajos científicos sobre el tema que han realizado científicos mexicanos.

Las aplicaciones de los AGs son muchas, y entre ellas podemos mencionar algunas como: el diseño de componentes automovilísticos, la automatización de los sistemas de comercio en el sector financiero, la logística en la carga de contenedores, el comportamiento de robots, la calibración y detección de daños en estructuras civiles, la bioinformática, la optimización de estructuras moleculares, la predicción del plegamiento de proteínas, la construcción de horarios en grandes universidades, y el problema del viajero ambulante entre otras.

Si algún lector quiere experimentar con el problema del viajero ambulante bajo el esquema de los algoritmos genéticos, se recomienda visitar la página http://www.obitko.com/tutorials/genetic-algorithms/tsp-example.php

Artículo publicado originalmente “Algoritmos genéticos” en el periódico Unión de Morelos por miembros de la Academia de Ciencias de Morelos A.C.