Orquestando un equipo de fútbol. Parte 1: Las bases matemáticas

El fútbol es un juego de equipo. ¡Claro!, no cabe ninguna duda. “Uno para todos, todos para uno”, o como se dice en Alemania, “11 amigos deben ser.” Es evidente que la defensa debe de cooperar con los jugadores del campo medio y ellos a su vez con los delanteros. Y no sólo eso, los sistemas modernos del fútbol son aún más flexibles y dependiendo de la situación que se presente en la cancha, los defensas podrían jugar un papel importante en el ataque, y no son raras las ocasiones en que ellos mismos anotan goles. A su vez, los delanteros pueden tomar temporalmente el papel de la defensa. Esta flexibilidad requiere que los jugadores “sientan” en cierta forma lo que están haciendo sus compañeros; sobre todo, deben intuir qué es lo que harán en el siguiente instante para poder actuar de manera óptima en beneficio del equipo.

Evidentemente, cada integrante del equipo juega de manera distinta a sus compañeros, pero lo hace en función estrictamente de lo que hacen los demás. Actualmente esto lo muestra casi a la perfección la selección de España. También el equipo de Alemania optimiza en buena medida esta dinámica colectiva, razón que les permitió ganar  con un marcador de 4:0 el juego contra Argentina durante  el último campeonato mundial, a pesar de que no contaban  con jugadores tan brillantes como, por ejemplo, Lionel Messi o Carlos Tévez.

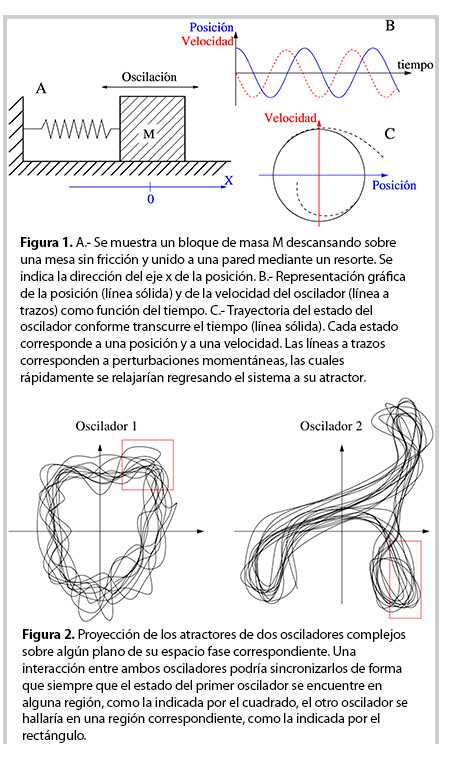
Los físicos estudian este tipo de fenómenos, a los cuales conocen como  “sincronización generalizada”, y los simulan numéricamente con ecuaciones diferenciales acopladas. Éstas son ecuaciones que relacionan a todas las cantidades que caracterizan al estado de un sistema en un momento dado con todas las cantidades que lo caracterizan en un tiempo anterior infinitamente cercano. La solución de estas ecuaciones suele mostrar oscilaciones irregulares, prácticamente impredecibles. Para ilustrar cómo podemos entender algunas propiedades de estos osciladores complejos empezaremos con una descripción gráfica de un oscilador simple, un bloque masivo que descansa sobre una mesa sin fricción, sujeto mediante un resorte a un punto fijo.

Imaginemos que alguien jala el bloque de masa M que  muestra la figura 1A una cierta distancia hacia el lado derecho, que designamos como la dirección “x”-positiva, y lo suelta. Entonces, el resorte estirado jalaría al bloque hacia la izquierda, haciéndolo adquirir una velocidad de magnitud creciente. Eventualmente, el bloque llegaría a su posición original x=0, su posición de equilibrio. A pesar de que en ella el resorte dejaría de jalar al bloque, éste seguiría su camino hacia la izquierda debido a su inercia, comprimiendo ahora al resorte hasta que la fuerza, que ahora éste ejercería hacia la derecha, lograra frenarlo. En este punto de retorno, correspondiente a un valor negativo de la posición x, la dirección del movimiento cambiaría y el resorte impulsaría al bloque ahora  hacía derecha. Esta secuencia se repetiría y el bloque iría y vendría de izquierda a derecha y de regreso, originando un  comportamiento oscilatorio que se  resume en la curva continua de la figura 1B, la cual muestra la coordenada x del bloque conforme transcurre el tiempo.

Consideremos ahora la velocidad del bloque. Ésta tendría el valor cero al inicio. Al soltar el bloque éste aumentaría gradualmente la rapidez de su movimiento. Como se movería hacia la izquierda, es decir, hacia la dirección negativa del eje x, el signo de su velocidad durante esta fase del movimiento sería negativo. La rapidez del bloque crecería hasta pasar por el punto x=0, el punto de equilibrio, a partir del cual disminuiría, el bloque se frenaría, hasta llegar a cero en el punto de retorno. Después la rapidez crecería de nuevo, pero ahora la velocidad sería positiva, dado que el bloque se movería hacia la derecha, es decir hacia la dirección x positiva. La curva a trazos de la figura 1B representa la evolución temporal de la velocidad. En la figura hemos ajustado las unidades de tal forma que los máximos y mínimos de las dos curvas estén al mismo nivel.

Se nota que cuando la posición, mostrada por la curva contínua, llega a sus valores extremos, a los puntos de retorno, la velocidad mostrada por la curva a trazos toma el valor cero, mientras que la velocidad encuentra sus extremos cuando el bloque pasa de ida o de vuelta por el punto de equilibrio, correspondiente a los ceros de la curva contínua. Por lo tanto, si hacemos una gráfica en la cual cada punto indique un estado del sistemacaracterizado por la posición y velocidad del bloque en un instante dado, como muestra la figura 1C, al transcurrir el tiempo, dicho punto recorrería una trayectoria circular. Figuras como la 1C se conocen como la representación del oscilador en el espacio fase.

Hasta ahora supusimos que no hay fricción ni ninguna otra  influencia del entorno sobre el oscilador. Sin embargo, llegaríamos a las mismas conclusiones si analizáramos este oscilador en presencia de una fuerza de fricción además de una fuerza externa que actúe periódicamente, como por ejemplo, si movieramos periódicamente hacia la izquierda y derecha la pared que muestra la figura 1A al lado izquierdo del resorte. También en este caso, una gráfica de la posición contra la velocidad del bloque formaría un círculo cuyo radio estaría determinado por la frecuencia de la fuerza externa, la elasticidad del resorte, el valor de la masa del bloque y la disipación debida a la fricción. Es más, si se perturbara en cierto momento al oscilador causando desviaciones respecto a su movimiento circular, como las ilustradas por las líneas interrumpidas en la figura  1C, el oscilador regresaría rápidamente al círculo. Se dice, que el círculo atrae a las trayectorias del sistema en el espacio fase, o bien, el círculo es el atractor del sistema.

Como se mencionó arriba, los osciladores complejos se describen matemáticamente a través de ecuaciones diferenciales acopladas. La solución de estas ecuaciones no es un número, como ocurre con ecuaciones algebraicas, sino funciones que describen la evolución temporal del sistema. Para el caso del oscilador armónico, las soluciones son las curva contínua y a trazos de la figura 1B, es decir, la posición y velocidad del bloque como función de tiempo. Entonces, resolviendo las ecuaciones se puede descubrir el atractor del sistema. El atractor de un sistema es un objeto característico del mismo. Si dos sistemas tuviesen el mismo atractor, su dinámica, es decir, su evolución conforme transcurre el tiempo, estaría regida por las mismas ecuaciones diferenciales y matemáticamente los dos sistemas serían equivalentes. Por ejemplo, el oscilador formado por una bloque y un resorte y un péndulo formado por una masa colgada de un hilo son sistemas matemáticamente equivalentes para oscilaciones de pequeña magnitud. Si Ud. mostrara un atractor de cierto sistema con forma de círculo o de elipse a un físico, de inmediato él le diría que el sistema correspondiente es un oscilador armónico.

Los atractores de osciladores complejos son usualmente objetos en un espacio fase de muchas dimensiones y su forma puede ser mucho mas complicada que un simple círculo (para una explicación simple de los espacios de muchas dimensiones, el lector podría ver los carteles de la exposición Laberintos Coordenados del Dr. Luis Mochán, disponibles en la página http://bit.ly/kPq4WP, y en particular, el cartel 2,http://bit.ly/13H3SYc). En la figura 2 se muestra una caricatura de cómo podría verse el atractor de dos osciladores complejos si se les proyecta sobre un plano.

Supongamos ahora que ponemos a los dos osciladores en cierto contacto de manera que interactúen entre sí, es decir, que cada sistema tenga alguna influencia sobre el otro. Imaginamos que hacemos el siguiente experimento. Escojamos una región cualquiera en el atractor del oscilador 1, como por ejemplo, la región marcada por el cuadrado arriba a la derecha, y midamos los tiempos en que el estado del oscilador 1 se encuentre dentro de dicha región. Si la interacción entre los dos osciladores fuese suficientemente fuerte, ocurriría el fenómeno de sincronización generalizada, en cuyo caso, se observaría que el estado del oscilador 2 se encontría durante esos tiempos también dentro de cierta región de su atractor, por ejemplo, el rectángulo abajo a la derecha. Esta sincronización no dependería de la elección de la primera región, la cual hicimos de manera arbitraria. Podríamos haber elegido cualquier otra región encima del atractor 1 y a ella correspondería alguna otra región del atractor 2, de forma que coincidirían los tiempos durante los cuales los estados de cada oscilador se hallasen en sus respectivas regiones.

Los dos osciladores podrían ser muy diferentes, la dimensión y la geometría de sus atractores podrían diferir, así como el comportamiento de ambos sistemas, y sin embargo, no actúan de manera independiente. La dinámica de uno puede estar relacionada fuertemente con la dinámica del otro y viceversa. Intuitivamente, puede esperarse que la probabilidad para que ocurra el fenómeno de sincronización generalizada será mayor cuando las frecuencias con las cuales ambos osciladores recorren su respectivo atractor sean  parecidas. Esta última observación es crucial para el planteamiento y la discusión de los resultados de un experimento que describiremos en la segunda parte de este artículo, en el cual aplicamos los conceptos discutidos en este artículo para estudiar el fenómeno de sincronización generalizada con equipos de futbol en Alemania.

Una versión corta de éste artículo se publicó en el Hypatia No. 45 www.hypatia.morelos.gob.mx.

Artículo publicado originalmente “Orquestando un equipo de fútbol. Parte 1: Las bases matemáticas” en el periódico Unión de Morelos por miembros de la Academia de Ciencias de Morelos A.C.